Sinds Newton weten wij dat bij gewone materie snelheden vectorieel bij elkaar opgeteld worden. Maar dit gebeurt ook bij licht, dat wil zeggen bij deeltjes verpakt in een golf.
Fotonen ontstaan in de onderstroom
Zoals wij gezien hebben bij HET ONTSTAAN VAN BEWEGING komt alle beweging tot stand omdat materie ‘op- en onderduikt’ in een onderstroom in de subta. De optelling van onderstromen verklaart de gebruikelijke vectoriële optelling van snelheden bij de interactie van gewone materie. Dat rotsblokken en kanonskogels, zoals Galilei constateerde, de snelheid van de aarde meekrijgen komt omdat de elementaire deeltjes waaruit deze aan de aarde gebonden materie bestaat voortdurend ‘op- en onderduikt’ in de sterke onderstroom van de aarde.
Maar ook bij fotonen speelt de onderstroom een rol. De productie van fotonen met een snelheid c vindt altijd plaats op het moment dat het desbetreffende atoom zich in de onderstroom bevindt. Het gevolg hiervan is dat een foton altijd al begint met de snelheid V die de bron op dat moment heeft. Wanneer de onderstroom zwak is wordt de resulterende snelheid c + V direct omgezet in een frequentieverandering (een Dopplereffect) en een snelheid c.
Wanneer de onderstroom voldoende sterk is (dit is waarschijnlijk al het geval bij een lichtbron met een massa > 10 kg) en er geen verstoring is door centrifugale stromingen (een lineaire beweging) behoudt een foton dat wordt uitgezonden door een bron met een snelheid V ook na het verlaten van de onderstroom gedurende enige tijd (ten hoogste enkele uren) de snelheid c‘ = c + V.
Deze snelheidsverandering geldt ook voor elektrische en magnetische velden
Ook de door bewegende (geladen) elementaire deeltjes uitgezonden elektrische en magnetische velden ontstaan in eerste instantie in de onderstroom. Daarom zal de normale snelheid c van elektrische en magnetische velden in alle richtingen, de snelheid van de onderstroom in die richting meekrijgen. Maar omdat het in dit geval niet – zoals bij een foton – ook om een deeltje gaat, maar slechts om stromingen in de subta zelf, zal dit effect makkelijker tot stand komen (ook bij een bron van een elektrisch of magnetisch veld met een gewicht < 10 kg). Het effect zal echter korter (slechts enkele seconden) duren.
Geen gevolgen van de snelheidsverandering voor de looptijd
Vanwege de ontstaanswijze van het heelal geldt in mijn theorie dat de ruimte absoluut is en dat beweging uiteindelijk altijd beweging is ten opzichte van het absolute referentiekader AFR (dat wil zeggen de gezamenlijke subta). Maar wij kunnen voor het gemak een willekeurig ander referentiekader kiezen. Wanneer wij spreken van ‘de aarde draait om de zon’ is impliciet de positie van de zon het referentiekader voor de bewegingen van de aarde en dus ook van alles dat op aarde beweegt.
De keuze van een ander referentiekader dan de aarde heeft niet alleen gevolgen voor de snelheid (snelheid is nu de snelheid ten opzichte van dit nieuwe referentiekader), maar ook voor de afgelegde weg (de afgelegde weg is de weg afgelegd ten opzichte van dit zelf gekozen referentiekader). Snelheid en afgelegde weg worden in gelijke mate veranderd. Het resultaat hiervan is dat de looptijd van een bewegend object in elk referentiekader hetzelfde is.
Wij zullen zien dat dit ook bij licht het geval is en dat de snelheidsverandering van het licht op deze manier de verandering in de lengte van de afgelegde weg camoufleert.
Een racebaan voor fotonen op aarde
In bijgaande twee figuren heb ik schetsmatig de situatie weergegeven van een racebaan op aarde, waarbij niet een paard maar een foton zich beweegt van een aan de aarde gebonden bron S naar een aan de aarde gebonden detector D. In de eerste figuur beweegt het foton zich in de richting van de beweging van de aarde rondom de zon (met de snelheid V) en daarna tegen de beweging van de aarde om de zon in (met de snelheid –V).
Het is belangrijk dat wij ons realiseren dat het hierbij steeds om het gelijk blijven van de looptijd van het licht gaat. De snelheden (zowel in longitudinale als in transversale richting) veranderen immers juist wél. Maar omdat door de beweging van de aarde de afstanden in gelijke mate veranderen, blijven de looptijden gelijk (zie ook hierna wat dit voor een observator op aarde betekent).
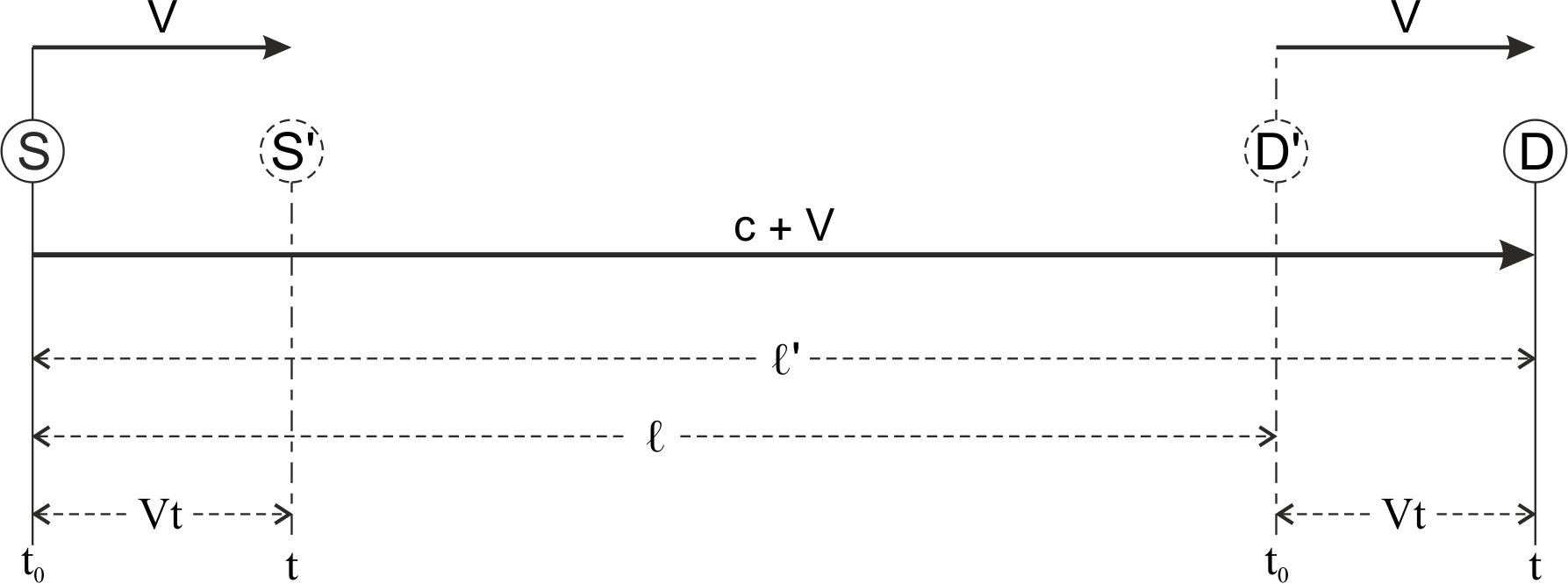
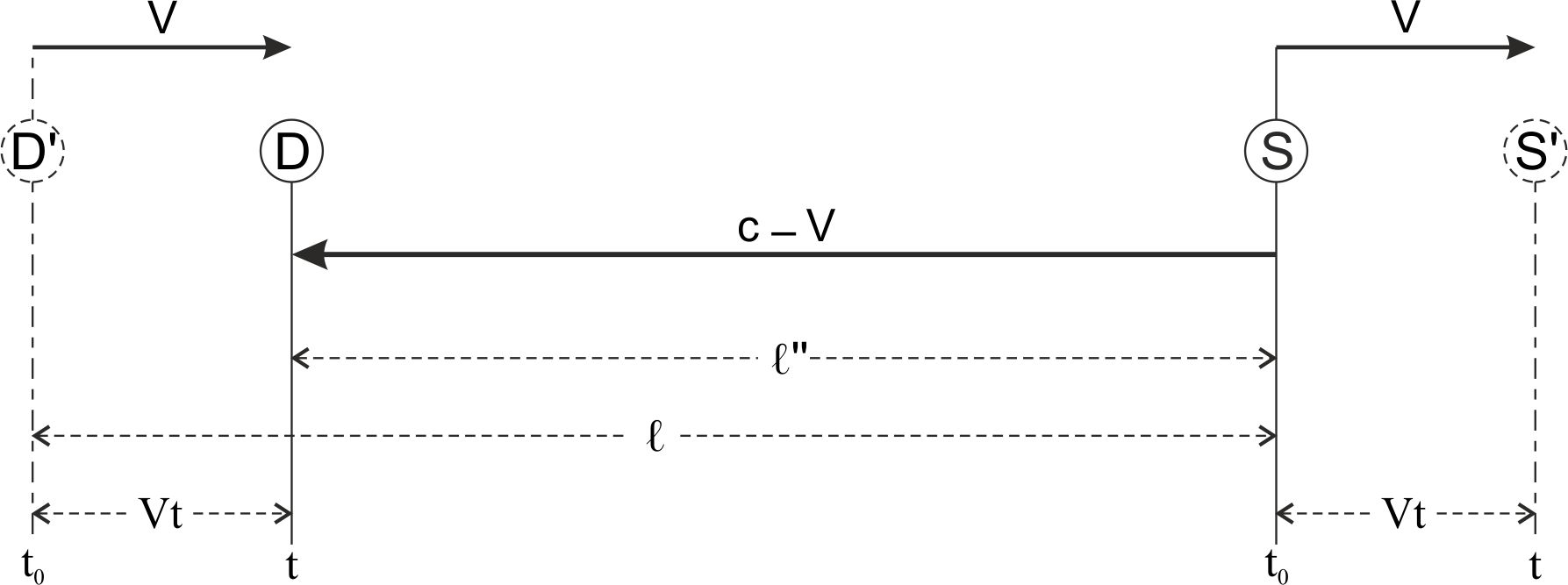
Deze eenvoudige formules gelden alleen voor een eenparige beweging van de lichtbron. Wanneer er sprake is van een lineaire versnelling treedt er waarschijnlijk ook een snelheidsverandering op, maar worden de formules voor de compensatie van een verandering in afgelegde weg door een snelheidsverandering ingewikkelder. Bij een roterende beweging is een snelheidsverandering van het licht onder invloed van een bewegende bron onmogelijk.
De snelheid van licht wordt altijd berekend
Wij stellen ons een observator op aarde voor die de in Fig. 2.4 en Fig. 2.5 (de nummers komen uit mijn boek) geschetste experimenten uitvoert en zichzelf de vraag stelt: Wat was in beide situaties de snelheid van het licht?
Het enige dat zij kan meten zijn de looptijd van het licht en de afstand in haar eigen referentiekader. Zij meet in beide gevallen een looptijd t = ℓ / c en controleert voor alle zekerheid de lengte van de afgelegde weg: de afstand tussen lichtbron en detector blijkt in beide gevallen ℓ te zijn.
Zij berekent vervolgens de snelheid van het licht: de snelheid = ℓ / t = ℓ / (ℓ / c ) = c. En haar conclusie is dat, onafhankelijk van de richting van de beweging van de aarde, de snelheid van het licht altijd gelijk is aan de lichtsnelheid c.
Zo wordt de, vanuit het absolute (of vanuit een ander) referentiekader gezien veranderde afgelegde weg, gecompenseerd door een evenredige verandering in de snelheid van het licht. Omdat wij de snelheid van het licht niet rechtstreeks kunnen meten en de looptijd altijd correct is, is een observator op aarde er ten onrechte van overtuigd dat de snelheid van het licht altijd gelijk is aan c.
Copyright © 2019 Ruimte, Beweging en Tijd: Drs. C.H.J.M. Opmeer
