HET ONTSTAAN VAN BEWEGING – Ruimte, Beweging en Tijd

Hoe kan er in deze wereld iets bewegen?

De hierboven beschreven gang van zaken levert een aantal problemen op voor het begrijpen van het verschijnsel bewegen zoals wij dat kennen:

Het ‘op- en onderduiken’ in de subta is iets anders dan ons bewegen. Wij kunnen het ‘op- en onderduiken’ in onze 3-D wereld op de grens van iets en niets zelfs niet waarnemen, omdat het plaats vindt langs de voor ons niet waarneembare 4e ruimtelijke dimensie van de subta.
De positie van de ‘op- en onder’ duikende elementaire deeltjes ten opzichte van de subta ligt vast en er is alleen een kleine variatie in de opduikpositie. Hiermee lijkt een beweging van de ene naar de andere positie in onze wereld (op de grens van de subtaruimte met het niets) onmogelijk.
Niet alleen het tot stand komen van een beweging, maar ook het blijven voortbestaan van een eenmaal in werking gezette beweging dient volgens mij verklaard te worden. De oude Grieken herkenden dit nog als een probleem, maar wij hebben er een wet van gemaakt en denken er dus niet meer over na.

Er is daarom een verklaring nodig zowel voor het tot stand komen als voor het blijven bestaan van een beweging.

Bewegen is uitsluitend mogelijk door ‘op- en onderduiken’ in een onderstroom

Ik veronderstel dat er bij het uitoefenen van een kracht op een elementair deeltje (een kracht die altijd nodig is om via een versnelling tot een eenparige beweging te komen), met behulp van de hierbij ‘onder water’ geleverde energie, een stroming in de subta tot stand komt met een snelheid V, waarbij de snelheid en de richting in overeenstemming zijn met de grootte en de richting van de uitgeoefende kracht.

De enige stroming in de subta die wij wat beter kennen, is de begeleidende golf van een altijd ‘onder water’ bewegend foton (zie onder Fotonen) en dit is een transversale golf. Ik ga er daarom van uit dat een dergelijke subtastroming, die ik onderstroom zal noemen, eveneens de vorm van een transversale golf heeft. Wanneer de transversale richting van de golf de richting heeft van de 4e dimensie van de subtaruimte blijft het contact met de grens bewaard en zal de golfvormige onderstroom zich parallel aan onze driedimensionale ruimte bewegen.

Wanneer een dergelijke stroming eenmaal tot stand is gebracht zal het deeltje, iedere keer als het ‘onderduikt’, in zijn onderstroom terecht komen en wordt het met een snelheid V meegevoerd en komt het bij het ‘opduiken’ op een andere positie in de grensruimte (dat wil zeggen in onze ruimte) weer boven. Omdat het ‘op- en onderduiken’ plaatsvindt met een snelheid c, kost het bijna geen tijd. De hoge intrinsieke frequentie zorgt ervoor dat het deeltje met de snelheid van de onderstroom in beweging blijft en daarmee zijn positie behoudt ten opzichte van andere elementaire deeltjes (bijvoorbeeld van een brok materie) die in dezelfde onderstroom ‘op- en onderduiken’. Omdat de onderstroom, als er geen andere krachten op werken, in de subta blijft bestaan, ontstaat er voor het elementaire deeltje een beweging die geheel voldoet aan de eerste bewegingswet van Newton.

Onderstromen kunnen van richting veranderen en worden samengevoegd of opgesplitst en gedragen zich in alle opzichten als vectoren, wat de bekende botsingswetten verklaart.

Toenemende weerstand tegen een verdere snelheidsverhoging

Het tot stand brengen van een onderstroom met een bepaalde snelheid in de subta kost al een bepaalde hoeveelheid energie. Maar de samenhangende subta zal weerstand bieden tegen een verdere verhoging van de snelheid van de onderstroom en dit zal bij en verdere verhoging dus steeds meer energie kosten. Naar het verband tussen de snelheidsverhoging van elektronen en de daarvoor vereiste energie werd al meer dan honderd jaar geleden onderzoek gedaan.

Een type experiment dat, vanaf het begin van de vorige eeuw, met steeds grotere nauwkeurigheid werd herhaald, is het afbuigen van snelle elektronen met behulp van sterke magneten. Deze experimenten werden voor het eerst uitgevoerd door Kaufmann (1901), die hiermee aantoonde dat de (inertiële) massa van elektronen, en daarmee dus ook de energie die nodig is om ze te versnellen, toenam naarmate de al eerder bereikte snelheid hoger was. Al snel werd duidelijk dat voor deze toename, de formule

1/ √ ( 1−V ²/c²) (1)

geldt en dat dus de limiet van de snelheidsverhoging de lichtsnelheid c is. Deze formule voor de toenemende weerstand bij een hoger wordende snelheid leidt, via een eenvoudige wiskundige bewerking, tot de bekende formule E = mc² voor de relatie tussen massa en energie.

Dat de natuurlijke snelheid van een transversale golf in de subta de snelheid c is, blijkt uit de snelheid van een foton. Dit is dus kennelijk ook de (onbereikbare) limiet van de snelheid van de eveneens golfvormige onderstroom.

Centrifugale beweging

Onderstromen zijn altijd lineair en bij een draaiende beweging, zoals van een roterende schijf, gebeurt er daarom ook iets speciaals. De onderstromen die de draaiing in stand houden worden alle opgewekt in de richting van de raaklijnen aan de draaicirkels van de schijf. Maar het subtamateriaal voor deze naar buiten gerichte rakende onderstromen moet steeds vanuit de subta aangevuld worden. Dit geeft een opeenhoping van subta die tot, vanuit het midden van de schijf naar buiten gerichte, subtastromen leidt. Deze, vanuit het middelpunt naar alle richtingen, in het vlak van de schijf naar buiten gerichte subtastromingen verklaren de bekende centrifugale verschijnselen.

De intrinsieke frequentie bij materie in beweging

Wat gebeurt er met de intrinsieke frequentie van een ‘op- en onderduikend’ elementair deeltje – bijvoorbeeld een uit gatdeeltjes opgebouwd atoom – wanneer het deeltje bovendien via een onderstroom beweegt? Ten gevolge van de meevoering door de onderstroom verandert dan de oorspronkelijke rechte weg (‘op en neer’) in een schuine weg. Ik heb de situatie geschetst in bijgaande Figuur 1-4.

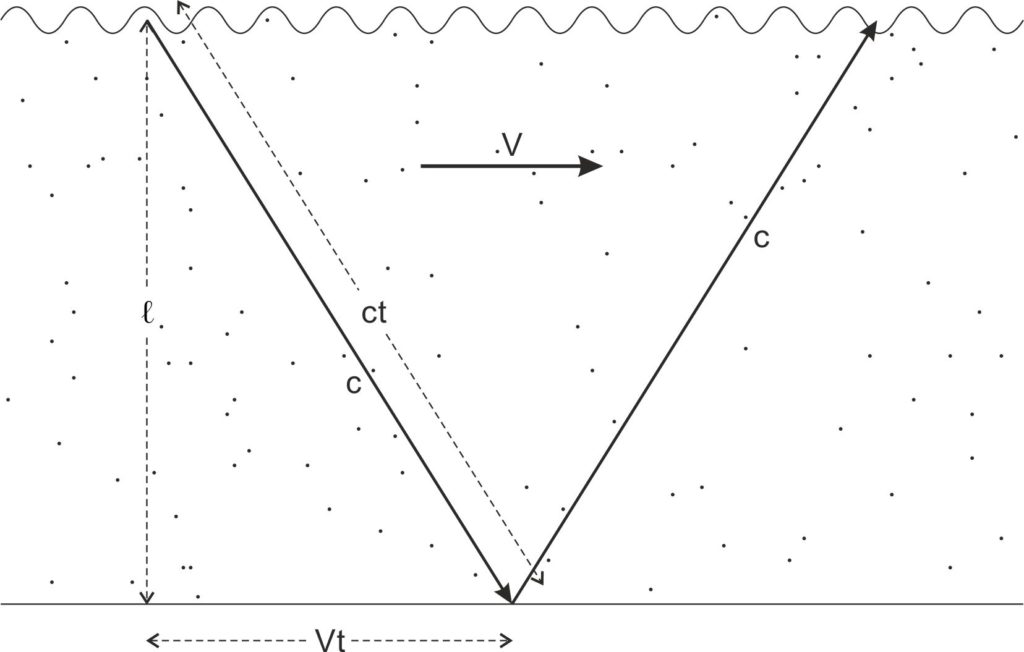
Fig. 1-4. Door de beweging van zijn onderstroom met een snelheid V, wordt het door een atoom bij zijn ‘op- en onderduiken’ in de subta afgelegde traject verlengd van een afstand 2 ℓ tot een afstand 2ct.

Klik hier voor de figuur 1-4 met een meer uitgebreide toelichting: Fig. 1-4 met legenda

Het deeltje, met zijn normale onderduiksnelheid c ten opzichte van de subta, ondergaat, in een met een snelheid V bewegende onderstroom, daarom een verlenging van de bij het ‘op- en onderduiken’ afgelegde weg met een factor 1/ √ ( 1−V ²/c²). Het gevolg van deze toename in afgelegde weg is, dat de tijdsduur die nodig is voor het afleggen van deze afstand met dezelfde waarde toeneemt en dat dus de intrinsieke frequentie van het deeltje verminderd wordt met een factor

√ ( 1 −V ²/ c²) . (2)

Gevolgen van het intrinsieke frequentie effect

De vertraging van de intrinsieke frequentie – vanwege de schuine weg bij het op- en onderduiken in de onderstroom die beweging mogelijk maakt – heeft gevolgen voor de meting van tijd en voor de totale frequentie van het door een bewegende bron uitgezonden licht (in aanvulling op het Dopplereffect):

Het leidt tot een verlaging van de bij een bepaald energieniveau horende lichtfrequentie. Hierdoor neemt ook de klokfrequentie van de (voor een nauwkeurige tijdmeting vereiste) atoomklok, bij een snelheid V ten opzichte van de subta, met een factor √ ( 1 −V ²/ c²) af. Een eenparige beweging in elke richting leidt dus tot een afname met deze factor van de gemeten tijd.
Een met een snelheid V bewegende lichtbron (of spiegel) leidt tot een hogere of lagere (bij een wijkende bron of spiegel) frequentie van het uitgezonden of gereflecteerde licht: het Dopplereffect. Maar beweging leidt ook tot een verlaging van de lichtfrequentie met een factor √ ( 1 −V ²/ c²) vanwege het intrinsieke frequentie effect. Een frequentieverandering van het uitgezonden licht ten gevolge van beweging is dan ook altijd een combinatie van het 1e orde Dopplereffect en het 2e orde intrinsieke frequentie effect. Dit laatste effect, dat onafhankelijk is van de richting van de beweging, wordt ten onrechte het “transversale Dopplereffect” genoemd, want het is geen Dopplereffect.

Referentie kaders

Er is al verschillende malen sprake geweest van een snelheid V, zonder dat duidelijk is gemaakt voor wie deze snelheid geldt. Waar dit van afhangt is het referentiekader van de observator die de beweging vaststelt. Voor een observator vormt de wereld (dat wil zeggen het uit een groot aantal elementaire deeltjes bestaande brok materie) waarop zij zich bevindt het referentiekader voor het vaststellen van beweging, ook wanneer het hele brok materie, inclusief de observator, zich eenparig voortbeweegt. De beoordeling door een observator of er iets beweegt en hoe snel het beweegt hangt af van de snelheid van de beweging ten opzichte van haar referentiekader.

Ik zal twee soorten referentiekaders onderscheiden:

Het ‘Moving Frame of Reference’ (MFR): Dit is een brok materie, waarvan alle onderdelen zich met dezelfde eenparige snelheid V voortbewegen ten opzichte van de gezamenlijke subta. Het eigen MFR vormt de vanzelfsprekende referentie om te beoordelen of bijvoorbeeld een brok steen of een trein in rust is of niet.
Het ‘Absolute Frame of Reference’ (AFR): Dit wordt gevormd door de gezamenlijke subta of door een brok materie dat in rust is ten opzichte van de subta. De gezamenlijke subta is de, voor ons niet rechtstreeks waarneembare, 4-D ruimte, die uiteindelijk als referentie dient voor elke beweging en dus ook voor beweging in onze wereld.

Dat mijn theorie leidt tot het bestaan van een absolute ruimte heeft een aantal voordelen:

Pas hierdoor is duidelijk wat beweegt ten opzichte van wat: bijvoorbeeld dat de trein stopt bij station Hilversum en niet omgekeerd.
Ook rotatie is nu een beweging ten opzichte van het AFR en niet ten opzichte van bijvoorbeeld de ‘vaste sterren’.
Een absolute ruimte maakt het bestaan van natuurconstanten beter begrijpelijk.

Maar het geeft ook grote problemen bij de nog tot laat in de 19e eeuw gangbare opvatting over de aard van licht (‘licht is een golf’) en het gedrag van dit licht op onze bewegende aarde. Dit leidde tot de speciale relativiteitstheorie. Zie voor een fysische oplossing van deze problemen onder LICHT EN BEWEGING.