DE TE STERKE ZWAARTEKRACHT WERKING – Ruimte, Beweging en Tijd

Het probleem van de te sterke zwaartekracht werking

Tegenwoordig is het volstrekt duidelijk dat, over grotere afstanden in het heelal, de werking van de zwaartekracht in hoge mate afwijkt van wat de formule van Newton voorspelt: de zwaartekrachtwerking over grote afstanden is veel sterker dan hij volgens Newton zou moeten zijn. De omloopsnelheid van de buitenste delen (bestaande uit sterren en gaswolken) van melkwegstelsels om het centrum bleek veel groter dan de totale hoeveelheid massa in het stelsel mogelijk maakte. Hetzelfde geldt voor de omloopsnelheid van de buitenste melkwegstelsels van clusters van melkwegstelsels. Ook de lenswerking over grote afstanden van een tussenliggende massa is veel sterker dan op grond van de zichtbare massa mogelijk zou zijn.

Een te vlakke rotatiecurve

Vanwege de afname van de zwaartekracht met een factor 1/ r ², neemt ook de rotatiesnelheid van objecten, naarmate de afstand tot het centrum groter wordt, steeds verder af. Dit wordt vaak weergegeven in de vorm van een rotatiecurve, die het verband aangeeft tussen de afstand vanaf het centrum op de x-as en de rotatiesnelheid op de y-as. Dit zou dus volgens Newton moeten leiden tot een curve die, vanaf het centrum van een melkwegstelsel naar buiten toe, een steeds kleiner wordende rotatiesnelheid voor de zich op die afstand bevindende objecten aangeeft. Dat wil zeggen, de rotatiecurves zouden moeten dalen. Over relatief kleine afstanden, zoals de afstanden binnen ons zonnestelsel, beschrijven de wetten van Kepler en van Newton de situatie uitstekend.

Maar, steeds weer blijkt dat dit niet geldt voor grote afstanden. Wanneer bijvoorbeeld de snelheid van objecten in melkwegstelsels wordt uitgezet tegen de afstand vanaf het centrum, zien wij dat de rotatiecurve te weinig daalt, of nagenoeg vlak blijft (of zelfs stijgt). Ik zal het probleem en de hiervoor tegenwoordig gebruikte oplossing illustreren aan de hand van een voorbeeld uit de praktijk. In figuur 4-3a wordt een door mij, op basis van een publicatie van Broeils (Broeils, A.H., Astron. Astrophys. 256, 19-32, 1992), gemaakte schets getoond van vier rotatiecurven van eenzelfde stelsel, waarvan er één op echte waarnemingsgegevens en drie op berekeningen zijn gebaseerd (met dank aan professor Martinus Veltman, die mij in een inspirerende lezing attent maakte op deze resultaten van Adrick Broeils). Op de horizontale as heb ik de afstanden vanaf het centrum in lichtjaren aangegeven.

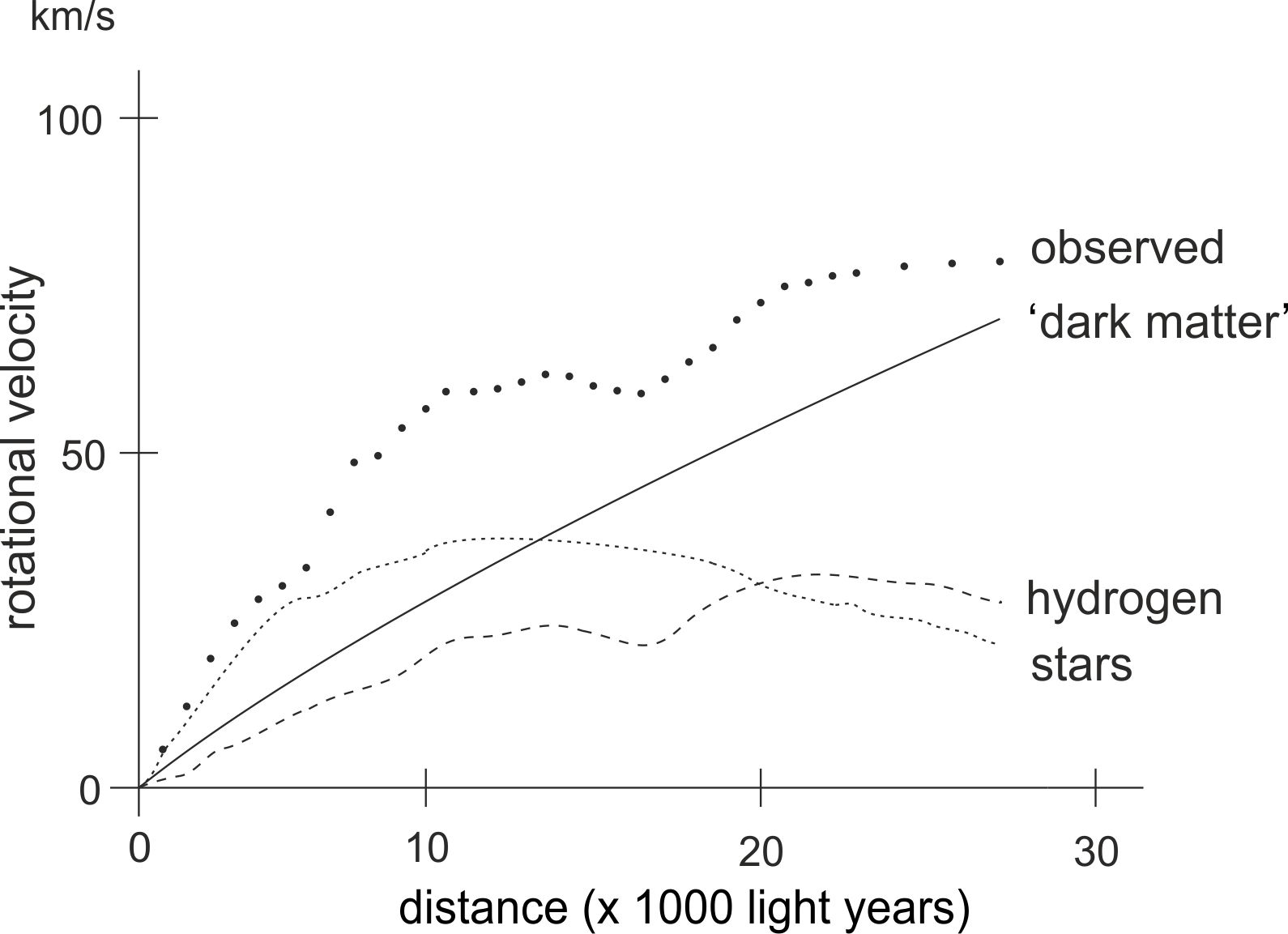
*Fig. 4-3a. Een schets van een aantal rotatiecurven van het kleine ellipsoïde stelsel NGC 1560, op basis van de gegevens van Broeils (Broeils, A.H., Astron. Astrophys.* **256***, 19-32, 1992).*

De gegevens hebben betrekking op een relatief klein stelsel, waarbij de buitenste roterende materie – op deze afstand in de vorm van waterstofwolken – zich op een afstand van bijna 30 000 lichtjaar vanaf het centrum bevindt. Op de verticale as staan de rotatiesnelheden aangegeven. De curve ‘observed’ wordt gevormd door de meetpunten van de feitelijk waargenomen rotatiesnelheden. De curven ‘stars’ en ‘hydrogen’ zijn gebaseerd op rotatiesnelheden die zijn berekend op basis van de massa van de waargenomen lichtgevende materie, respectievelijk van de waargenomen waterstof. Het is duidelijk dat de op basis van de in feite aanwezige massa berekende rotatiesnelheden al op een afstand van enige duizenden lichtjaren veel lager zouden moeten zijn dan de op deze afstand (en na deze tijd!) waargenomen rotatiesnelheden. De waargenomen rotatiesnelheid (de curve ‘observed’) vertoont naar de periferie toe zelfs een verdere stijging, wat lijkt te wijzen op een veel grotere massa dan er in feite in dit stelsel aanwezig is.

Ook een te sterke lenswerking

Er is nog een ander verschijnsel, dat wijst op een te sterke zwaartekrachtwerking op veel plaatsen in het heelal. Omdat het licht iets wordt afgebogen door de zwaartekracht (zie onder ZWAARTEKRACHT EN FOTONEN) fungeert een vanaf de aarde gezien tussenliggende massa als een lens voor ver weg gelegen stelsels en objecten. Uit de sterkte van de lenswerking kan de grootte van de tussenliggende massa berekend worden. Het blijkt nu dat de waargenomen tussenliggende massa vaak niet in staat is om de in feite optredende lenswerking te kunnen verklaren: de lenswerking is daarvoor veel te sterk. Ook in dit geval lijkt de waargenomen massa in veel gevallen te gering om de grootte van de effecten (over nog veel grotere afstanden dan de afstanden binnen een melkwegstelsel) te kunnen verklaren.

‘Donkere materie’ zou voor extra massa zorgen

Toen men de te vlakke rotatiecurven niet kon verklaren was de conclusie al snel dat er dan wel een grote hoeveelheid onzichtbare massa moest zijn, die men ‘donkere materie’ noemde. In figuur 4-3a geeft de geconstrueerde curve ”dark matter” aan hoe groot de bijdrage van de veronderstelde ‘donkere materie’ zou moeten zijn om de waargenomen rotatiesnelheden (de curve ‘observed’) te kunnen verklaren. Het is duidelijk dat deze onbekende massa aanzienlijk zou moeten zijn en dat, op een wat grotere afstand van het centrum, deze onbekende massa de hoeveelheid bekende massa zelfs zou overtreffen.

De veronderstelling is (en dat is nu al weer vele jaren zo) dat elk melkwegstelsel en elke cluster van melkwegstelsels wordt omgeven door een bolvormige halo, bestaande uit een grote hoeveelheid onzichtbare en na ruim meer dan 80 jaar nog steeds, wat zijn aard en samenstelling betreft, onbekende, ‘donkere materie’.