Polarisators
Er bestaan transparante kristallijne, materialen die alleen licht doorlaten waarvan de fotonen een bepaalde polarisatierichting hebben. Een dergelijk materiaal, bijvoorbeeld in de vorm van een schijfje waarvan de polarisatiehoek kan worden ingesteld, wordt een polarisatie analysator of kortweg een polarisator genoemd. Hoe groter het verschil tussen de polarisatierichting van het licht en de polarisatiehoek van de polarisator hoe kleiner het percentage van het licht dat wordt doorgelaten (volgens de wet van Malus). Of een individueel foton al of niet wordt doorgelaten is, volgens de huidige opvatting, een kwestie van toeval.
Wanneer een bepaalde hoeveelheid licht eenmaal een polarisator met een bepaalde polarisatiehoek is gepasseerd zal 100% van dat licht ook door een volgende polarisator met dezelfde polarisatiehoek worden doorgelaten.
Het doorlaten van een foton door een polarisator is geen toeval
Ik heb een foton opgevat als een golf met een echt deeltje en dit deeltje met zijn intrinsieke spin levert een belangrijke bijdrage aan de totale polarisatie van een foton. Omdat normale fotonen juist in dit opzicht van elkaar verschillen is het duidelijk dat het al of niet doorgelaten worden van een bepaald foton geen toeval kan zijn. Of een foton wordt doorgelaten door een polarisator met een bepaalde polarisatiehoek wordt bepaald door de totale fotonpolarisatie, en daarvan vooral door de intrinsieke spin van het fotondeeltje.
Een eventueel (klein) verschil in golfpolarisatie wordt aangepast, maar de intrinsieke spin van het fotondeeltje blijft bij de doorgang door het materiaal van de polarisator behouden.
Gelijke fotonen worden door eenzelfde polarisator gelijk behandeld
Twee identieke fotonen hebben niet alleen dezelfde polarisatie van de fotongolf, maar ook dezelfde intrinsieke spin van het fotondeeltje en de fotondeeltjes hebben bovendien ook precies dezelfde grootte. Daarom worden twee gelijke fotonen die bovendien voor een polarisator gelijk zijn (dat wil zeggen in dezelfde fase en met eenzelfde momentum) door eenzelfde type polarisator met hetzelfde materiaal óf beide doorgelaten óf beide geabsorbeerd.
Het Aspect experiment
Een van de eerste quantumoptische experimenten, waarbij gebruik gemaakt werd van paarsgewijs geproduceerde, nagenoeg gelijke, afzonderlijke fotonen, werd in 1982 uitgevoerd door Alain Aspect en zijn medewerkers. Later is het experiment in verschillende vormen herhaald maar nu met, van ‘down conversie’ afkomstige, paren identieke fotonen.
Vanuit de bron worden steeds twee horizontaal gepolariseerde (H = 0°) en ook verder in hoge mate gelijke fotonen naar een eigen op eenzelfde afstand geplaatste polarisator gezonden (zie de bijgaande figuur). Geteld werd hoe vaak de achter de polarisators geplaatste, speciaal voor het detecteren van afzonderlijke fotonen ontworpen, detectors gelijktijdig een foton detecteerden. Dit leverde een correlatie op die kon variëren van 0 (= geen enkele coïncidentie) tot 1 (= steeds detecteerden beide detectors tegelijkertijd een foton).
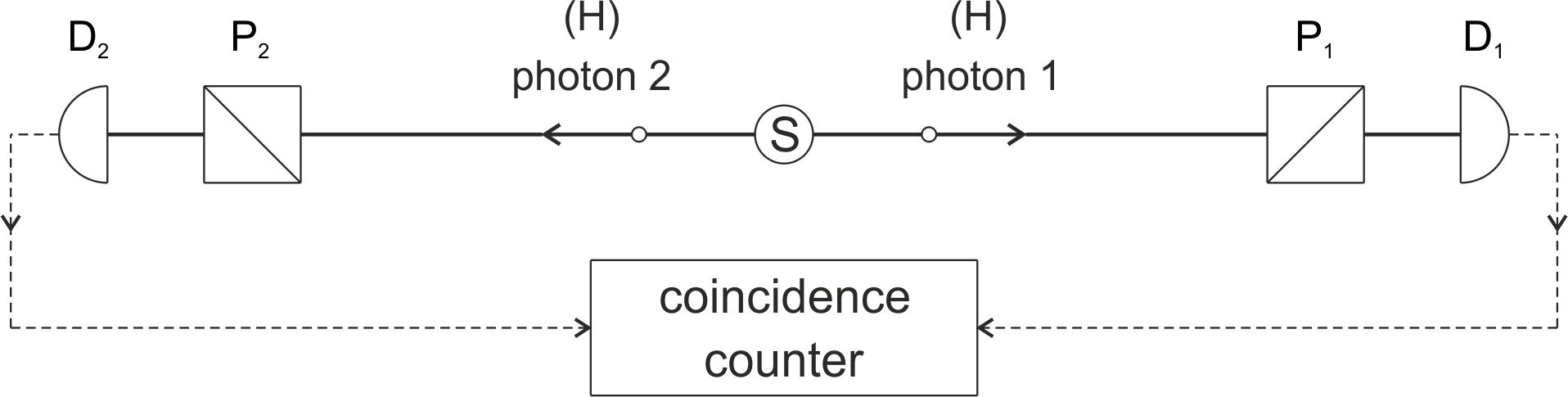
Fig. 3-3. De basisopstelling in het Aspect experiment (Aspect et al., 1982).
De bron S genereert paren in hoge mate gelijke, beide horizontaal (H) gepolariseerde, afzonderlijke fotonen (aangegeven door cirkeltjes) en zendt steeds één foton in de ene richting en één foton in de andere richting. Voor de detectors D1 en D2 zijn de met verschillende hoekwaarden instelbare polarisators P1 en P2 geplaatst. Het aantal coïncidenties (detectie van een foton door beide detectors binnen een tijd van 20 ns) wordt geteld door de coïncidentie ‘counter’.
Eerst werden beide polarisators ingesteld op de in dit type onderzoek vaak gebruikte hoek van 45°. Volgens de huidige opvatting, waarbij de kans dat een polarisator een foton doorlaat geheel is bepaald door toeval, zou dit een correlatie = 0,5 moeten opleveren. Volgens mijn ‘gelijke behandeling van gelijke fotonen’ zou de correlatie = 1 moeten zijn. Als de ene polarisator een foton doorlaat zou de ander het ook moeten doen en omgekeerd.
Ook werden de beide polarisators met een aantal verschillende hoeken ingesteld, waarbij steeds berekend werd wat de correlatie zou zijn bij de veronderstelde werking volgens toeval van het doorlaten van fotonen.
Bell’s ongelijkheid
Het ging Aspect echter niet om het vinden van de precieze correlaties bij de verschillende ingestelde hoeken, maar om het testen van de zogenaamde ongelijkheid van Bell. Volgens de formule van John Bell zou een bepaalde, op de correlaties gebaseerde grootheid S, op grond van klassieke overwegingen, niet overschreden kunnen worden. Aspect moest echter constateren, evenals vele onderzoekers na hem, dat zijn correlaties steeds significant te groot waren. Dit werd algemeen geïnterpreteerd als een ondersteuning van de quantumopvatting. Mijn hierboven gegeven verklaring van de hoge correlaties als een gevolg van de gelijke behandeling door een polarisator van gelijke fotonen, bewijst echter dat ook een rationele fysische opvatting mogelijk is.
Dit leidt tot een nieuw experiment om mijn theorie te toetsen in de vorm van een Aspect experiment met gelijke afstanden naar de polarisators, maar met ongelijke afstanden naar de beide erachter liggende detectors (zie onder TOETSINGSEXPERIMENT 11).
Volgens de huidige opvatting zullen ook in deze opstelling de gevonden correlaties laag zijn omdat, indien gewenst, steeds nagegaan kan worden welk foton bij welke detector aankomt. Volgens de hier gegeven verklaring zullen de correlaties hoog zijn omdat de beide een-van-een-paar fotonen in dezelfde fase eenzelfde type polarisator (met hetzelfde materiaal) treffen en dus steeds gelijk behandeld worden: ze worden daarom beide doorgelaten of beide tegengehouden.
Met deze opstelling is het dus mogelijk om mijn stelling te toetsen, dat het niet de gelijktijdigheid (en dus ononderscheidbaarheid) voor de detectors, maar de gelijkheid van de beide fotonen voor de polarisators (en de daaruit voortvloeiende gelijke behandeling) is, die bepaalt of er een hoge correlatie ontstaat.
Copyright © 2019 Ruimte, Beweging en Tijd: Drs. C.H.J.M. Opmeer
